STPSAKAP.ac.id

Memahami Cermin Cekung: Panduan Lengkap dan Contoh Soal untuk Kelas 3 SMP

Pernahkah Anda memperhatikan bagaimana sendok bagian dalam memantulkan bayangan Anda terbalik? Atau bagaimana cermin rias membuat wajah Anda terlihat lebih besar? Itu adalah contoh sederhana dari prinsip kerja cermin cekung. Dalam fisika, cermin cekung adalah salah satu topik yang menarik dan sering muncul dalam ujian. Artikel ini akan membawa Anda menyelami dunia cermin cekung, memahami konsep dasarnya, rumus-rumus penting, hingga langkah-langkah praktis dalam menyelesaikan soal-soalnya.

I. Pengantar: Apa Itu Cermin Cekung?

Cermin adalah permukaan yang dapat memantulkan cahaya. Cermin cekung adalah jenis cermin sferis (berbentuk bola) yang permukaannya melengkung ke dalam, seperti bagian dalam sendok. Karena bentuknya yang demikian, cermin cekung memiliki kemampuan unik untuk mengumpulkan sinar cahaya (konvergen) pada satu titik. Inilah mengapa cermin cekung banyak digunakan dalam aplikasi sehari-hari seperti:

• Cermin rias/cukur: Untuk memperbesar bayangan wajah.
• Lampu senter atau lampu depan mobil: Untuk mengumpulkan cahaya dari bohlam dan memancarkannya sebagai berkas sejajar yang kuat.
• Reflektor teleskop: Untuk mengumpulkan cahaya dari benda-benda langit yang sangat jauh.
• Cermin gigi: Untuk melihat bagian dalam mulut pasien dengan lebih jelas.

Memahami bagaimana cermin cekung membentuk bayangan sangat penting. Tidak hanya untuk nilai di sekolah, tetapi juga untuk memahami fenomena cahaya di sekitar kita.

II. Konsep Dasar Cermin Cekung yang Perlu Diketahui

Sebelum kita melangkah ke rumus dan soal, mari kita kenali beberapa istilah penting yang berkaitan dengan cermin cekung:

1. Sumbu Utama (Principal Axis): Garis lurus yang melewati pusat cermin dan titik fokusnya.
2. Titik Pusat Optik (O/P): Titik tengah cermin tempat sumbu utama memotong permukaan cermin.
3. Pusat Kelengkungan (C): Pusat bola imajiner dari mana cermin cekung ini "dipotong". Jarak dari C ke cermin sama dengan jari-jari kelengkungan.
4. Jari-jari Kelengkungan (R): Jarak dari Pusat Kelengkungan (C) ke permukaan cermin.
5. Titik Fokus (F): Titik pada sumbu utama di mana sinar-sinar cahaya sejajar yang datang menuju cermin akan berkumpul setelah dipantulkan.
6. Jarak Fokus (f): Jarak dari Titik Fokus (F) ke Titik Pusat Optik (O/P). Untuk cermin cekung, jarak fokus selalu positif karena titik fokusnya nyata.

Hubungan Penting:
Untuk cermin cekung, titik fokus (F) selalu berada di tengah-tengah antara Titik Pusat Optik (O) dan Pusat Kelengkungan (C). Ini berarti:
R = 2f atau f = R/2

III. Sinar-Sinar Istimewa pada Cermin Cekung

Untuk memahami pembentukan bayangan, kita menggunakan sinar-sinar istimewa. Ada tiga sinar istimewa yang sangat membantu dalam melukis bayangan dan memverifikasi perhitungan kita:

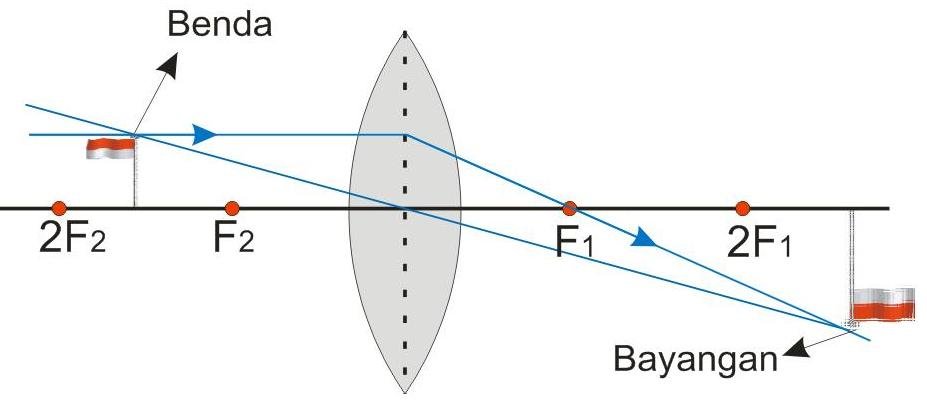
1. Sinar datang sejajar sumbu utama: Akan dipantulkan melalui titik fokus (F).
2. Sinar datang melalui titik fokus (F): Akan dipantulkan sejajar sumbu utama.
3. Sinar datang melalui pusat kelengkungan (C): Akan dipantulkan kembali melalui titik pusat kelengkungan (C) itu sendiri.

Dengan menggunakan setidaknya dua dari tiga sinar istimewa ini, kita dapat menentukan letak dan sifat bayangan yang terbentuk.

IV. Sifat Bayangan yang Dibentuk Cermin Cekung

Sifat bayangan yang terbentuk oleh cermin cekung sangat tergantung pada letak benda terhadap cermin. Mari kita rangkum dalam tabel berikut:

No.	Letak Benda	Letak Bayangan	Sifat Bayangan
1	Di Tak Hingga	Di titik F	Nyata, Terbalik, Diperkecil
2	Di luar C	Antara F dan C	Nyata, Terbalik, Diperkecil
3	Tepat di C	Tepat di C	Nyata, Terbalik, Sama Besar
4	Antara F dan C	Di luar C	Nyata, Terbalik, Diperbesar
5	Tepat di F	Di Tak Hingga	Tidak terbentuk bayangan
6	Antara F dan O	Di belakang cermin	Maya, Tegak, Diperbesar

Catatan:

• Nyata: Bayangan yang terbentuk dari perpotongan langsung sinar pantul dan dapat ditangkap oleh layar. Selalu terbalik.
• Maya: Bayangan yang terbentuk dari perpotongan perpanjangan sinar pantul dan tidak dapat ditangkap oleh layar. Selalu tegak.

V. Rumus-Rumus Penting untuk Perhitungan Cermin Cekung

Untuk menyelesaikan soal-soal perhitungan, kita akan menggunakan dua rumus utama:

1. Rumus Hubungan Jarak Benda, Jarak Bayangan, dan Jarak Fokus:
   1/f = 1/s + 1/s’
   Dimana:

   • f = jarak fokus cermin (selalu positif untuk cermin cekung)
   • s = jarak benda ke cermin (selalu positif)
   • s' = jarak bayangan ke cermin

   Konvensi Tanda untuk s’:

   • Jika s' bernilai positif (+), bayangan bersifat nyata (terletak di depan cermin, di sisi yang sama dengan benda).
   • Jika s' bernilai negatif (-), bayangan bersifat maya (terletak di belakang cermin, berlawanan sisi dengan benda).

2. Rumus Perbesaran Bayangan (M):
   M = |s’/s| = h’/h
   Dimana:

   • M = perbesaran bayangan (tidak memiliki satuan)
   • s' = jarak bayangan
   • s = jarak benda
   • h' = tinggi bayangan
   • h = tinggi benda

   Interpretasi Nilai M:

   • Jika M > 1, bayangan diperbesar.
   • Jika M < 1 (misal 0.5), bayangan diperkecil.
   • Jika M = 1, bayangan sama besar dengan benda.

   Konvensi Tanda untuk h’ (opsional, tergantung konteks soal):

   • Jika h' bernilai positif (+), bayangan bersifat tegak.
   • Jika h' bernilai negatif (-), bayangan bersifat terbalik.
     (Perlu diingat bahwa dalam rumus perbesaran M = |s’/s|, kita menggunakan nilai mutlak, sehingga M selalu positif. Untuk mengetahui sifat tegak/terbalik, kita perlu melihat tanda s' atau melukis sinar.)

VI. Contoh Soal Cermin Cekung dan Pembahasannya

Mari kita terapkan konsep dan rumus yang telah kita pelajari ke dalam beberapa contoh soal.

Contoh Soal 1: Mencari Jarak Bayangan dan Sifatnya

Soal:
Sebuah benda setinggi 4 cm diletakkan 30 cm di depan cermin cekung yang memiliki jari-jari kelengkungan 20 cm. Tentukan:
a. Jarak fokus cermin.
b. Jarak bayangan yang terbentuk.
c. Perbesaran bayangan.
d. Tinggi bayangan.
e. Sifat bayangan yang terbentuk.

Diketahui:

• Tinggi benda (h) = 4 cm
• Jarak benda (s) = 30 cm
• Jari-jari kelengkungan (R) = 20 cm

Ditanya:
a. Jarak fokus (f)
b. Jarak bayangan (s’)
c. Perbesaran (M)
d. Tinggi bayangan (h’)
e. Sifat bayangan

Penyelesaian:

a. Jarak fokus (f):
Kita tahu bahwa f = R/2
f = 20 cm / 2
f = 10 cm

b. Jarak bayangan (s’):
Gunakan rumus 1/f = 1/s + 1/s’
1/10 = 1/30 + 1/s’
1/s’ = 1/10 – 1/30
Untuk mengurangkan pecahan, samakan penyebutnya (KPK dari 10 dan 30 adalah 30):
1/s’ = 3/30 – 1/30
1/s’ = 2/30
1/s’ = 1/15
s’ = 15/1
s’ = 15 cm

c. Perbesaran bayangan (M):
Gunakan rumus M = |s’/s|
M = |15 cm / 30 cm|
M = 0.5
M = 0.5 kali

d. Tinggi bayangan (h’):
Gunakan rumus M = h’/h
0.5 = h’ / 4 cm
h’ = 0.5 * 4 cm
h’ = 2 cm

e. Sifat bayangan:

• Karena s' bernilai positif (+15 cm), bayangan bersifat nyata.
• Karena s' positif, bayangan juga bersifat terbalik (sesuai sifat bayangan nyata).
• Karena M < 1 (0.5), bayangan bersifat diperkecil.
• (Untuk memverifikasi, letak benda 30 cm > R=20cm (yaitu > C). Sesuai tabel, benda di luar C menghasilkan bayangan Nyata, Terbalik, Diperkecil, dan terletak antara F dan C. Jarak s’=15 cm, yang memang antara F=10 cm dan C=20 cm. Cocok!)

Kesimpulan: Bayangan yang terbentuk berjarak 15 cm di depan cermin, memiliki tinggi 2 cm, dan bersifat nyata, terbalik, diperkecil.

Contoh Soal 2: Benda di Antara F dan C

Soal:
Sebuah cermin cekung memiliki jarak fokus 12 cm. Jika sebuah lilin diletakkan 18 cm di depan cermin tersebut, tentukan:
a. Jarak bayangan yang terbentuk.
b. Sifat bayangan.
c. Perbesaran bayangan.

Diketahui:

• Jarak fokus (f) = 12 cm
• Jarak benda (s) = 18 cm

Ditanya:
a. Jarak bayangan (s’)
b. Sifat bayangan
c. Perbesaran (M)

Penyelesaian:

a. Jarak bayangan (s’):
Gunakan rumus 1/f = 1/s + 1/s’
1/12 = 1/18 + 1/s’
1/s’ = 1/12 – 1/18
Samakan penyebut (KPK dari 12 dan 18 adalah 36):
1/s’ = 3/36 – 2/36
1/s’ = 1/36
s’ = 36/1
s’ = 36 cm

b. Sifat bayangan:

• Karena s' bernilai positif (+36 cm), bayangan bersifat nyata.
• Bayangan nyata selalu terbalik.
• Untuk mengetahui diperbesar atau diperkecil, kita hitung perbesaran.

c. Perbesaran bayangan (M):
Gunakan rumus M = |s’/s|
M = |36 cm / 18 cm|
M = 2 kali

• Karena M > 1 (2 kali), bayangan bersifat diperbesar.
• (Untuk memverifikasi, letak benda 18 cm. Jarak fokus f=12 cm, maka C=2f=24 cm. Benda 18 cm berarti berada di antara F dan C (12 cm < 18 cm < 24 cm). Sesuai tabel, benda antara F dan C menghasilkan bayangan Nyata, Terbalik, Diperbesar, dan terletak di luar C. Jarak s’=36 cm, yang memang di luar C=24 cm. Cocok!)

Kesimpulan: Bayangan yang terbentuk berjarak 36 cm di depan cermin, dan bersifat nyata, terbalik, diperbesar.

Contoh Soal 3: Benda di Antara F dan O (Bayangan Maya)

Soal:
Seorang anak melihat wajahnya pada cermin rias yang memiliki jarak fokus 25 cm. Jika wajah anak tersebut berjarak 10 cm dari cermin, tentukan:
a. Jarak bayangan wajah anak.
b. Perbesaran bayangan.
c. Sifat bayangan.

Diketahui:

• Jarak fokus (f) = 25 cm
• Jarak benda (s) = 10 cm

Ditanya:
a. Jarak bayangan (s’)
b. Perbesaran (M)
c. Sifat bayangan

Penyelesaian:

a. Jarak bayangan (s’):
Gunakan rumus 1/f = 1/s + 1/s’
1/25 = 1/10 + 1/s’
1/s’ = 1/25 – 1/10
Samakan penyebut (KPK dari 25 dan 10 adalah 50):
1/s’ = 2/50 – 5/50
1/s’ = -3/50
s’ = -50/3
s’ ≈ -16.67 cm

b. Perbesaran bayangan (M):
Gunakan rumus M = |s’/s|
M = |-16.67 cm / 10 cm|
M = 1.667
M ≈ 1.67 kali

c. Sifat bayangan:

• Karena s' bernilai negatif (-16.67 cm), bayangan bersifat maya.
• Bayangan maya selalu tegak.
• Karena M > 1 (1.67 kali), bayangan bersifat diperbesar.
• (Untuk memverifikasi, letak benda 10 cm. Jarak fokus f=25 cm. Benda 10 cm berarti berada di antara F dan O (10 cm < 25 cm). Sesuai tabel, benda antara F dan O menghasilkan bayangan Maya, Tegak, Diperbesar, dan terletak di belakang cermin. Jarak s’=-16.67 cm, yang memang di belakang cermin. Cocok!)

Kesimpulan: Bayangan wajah anak tersebut berjarak sekitar 16.67 cm di belakang cermin, dan bersifat maya, tegak, diperbesar. Ini menjelaskan mengapa cermin rias membuat wajah terlihat lebih besar.

Contoh Soal 4: Menentukan Jarak Benda dari Perbesaran

Soal:
Sebuah benda diletakkan di depan cermin cekung yang memiliki jarak fokus 15 cm. Jika bayangan yang terbentuk nyata dan diperbesar 3 kali, tentukan jarak benda tersebut dari cermin.

Diketahui:

• Jarak fokus (f) = 15 cm
• Perbesaran (M) = 3 kali
• Sifat bayangan: nyata (berarti s’ positif)

Ditanya:
Jarak benda (s)

Penyelesaian:

Kita punya dua rumus:

1. 1/f = 1/s + 1/s’
2. M = |s’/s|

Dari rumus perbesaran:
M = s’/s (karena bayangan nyata, s’ positif)
3 = s’/s
s’ = 3s

Sekarang substitusikan s' = 3s ke rumus hubungan jarak:
1/f = 1/s + 1/s’
1/15 = 1/s + 1/(3s)
Samakan penyebut di ruas kanan (KPK dari s dan 3s adalah 3s):
1/15 = 3/(3s) + 1/(3s)
1/15 = 4/(3s)

Sekarang kita bisa menyelesaikan untuk s:
3s = 4 * 15
3s = 60
s = 60 / 3
s = 20 cm

Kesimpulan: Jarak benda dari cermin adalah 20 cm.

Verifikasi:
Jika s=20 cm dan f=15 cm, maka benda berada di antara F (15 cm) dan C (2f=30 cm). Sesuai tabel, benda di antara F dan C menghasilkan bayangan nyata, terbalik, dan diperbesar. Ini cocok dengan informasi di soal. Mari hitung s’ dan M-nya:
1/s’ = 1/f – 1/s = 1/15 – 1/20 = 4/60 – 3/60 = 1/60 => s’ = 60 cm.
M = s’/s = 60/20 = 3 kali. Cocok!

VII. Tips Sukses Mengerjakan Soal Cermin Cekung

1. Pahami Konsep Dasar: Jangan terburu-buru menghafal rumus. Pahami dulu apa itu f, C, R, s, s’, serta sinar-sinar istimewa dan sifat bayangan.
2. Perhatikan Konvensi Tanda: Ini adalah kunci! Kesalahan tanda adalah penyebab utama kesalahan perhitungan. Ingat: f cermin cekung selalu positif, s selalu positif, s’ positif untuk nyata, s’ negatif untuk maya.
3. Gambarkan Diagram (Opsional tapi Direkomendasikan): Meskipun tidak diminta, melukis bayangan dengan sinar istimewa dapat membantu memverifikasi hasil perhitungan Anda dan memberi Anda gambaran visual.
4. Tulis "Diketahui" dan "Ditanya": Ini membantu Anda mengorganisir informasi dan memastikan tidak ada yang terlewat.
5. Langkah Demi Langkah: Jangan mencoba menghitung semuanya dalam satu baris. Kerjakan secara bertahap: cari f, lalu s’, lalu M, lalu h’.
6. Periksa Kembali: Setelah mendapatkan jawaban, tanyakan pada diri sendiri: "Masuk akal tidak hasil ini dengan sifat bayangan yang seharusnya?" (Misalnya, jika benda di antara F dan O, bayangan harus maya dan diperbesar. Jika perhitungan Anda menghasilkan nyata dan diperkecil, berarti ada yang salah.)

VIII. Penutup

Cermin cekung adalah topik yang fundamental dalam optika. Dengan memahami konsep dasarnya, menghafal rumus, dan berlatih dengan berbagai jenis soal, Anda akan menguasai materi ini dengan mudah. Ingatlah bahwa fisika bukan hanya tentang angka, tetapi juga tentang pemahaman bagaimana dunia di sekitar kita bekerja. Teruslah berlatih dan jangan ragu untuk bertanya jika ada yang kurang jelas. Selamat belajar!